Klassifikationsleistung Klassifikators
Konfusionsmatrix
Bewertung der Klassifizierungsleistung
In BCI-Anwendungen wie auch in anderen Anwendungen von Klassifikatoren ist es wichtig, die Genauigkeit eines ausgewählten Klassifikators zu bewerten. Im Folgenden werden wir einige der wichtigsten Bewertungskriterien vorstellen.Konfusionsmatrix
Zur Auswertung der Leistung ist es hilfreich, die Einträge einer Konfusionsmatrix zu untersuchen. Für binäre (wahr oder falsch) Probleme handelt es sich hierbei um eine 2x2 Matrix. Die vier Einträge der Matrix entsprechen:- TP (engl. True Positives) - Richtig positiv: die Anzahl der korrekten positiven Klassifizierungen (Treffer)
- FN (engl. False Negatives) - Falsch Negativ: die Anzahl der positiven Klassifizierungen die fälschlicherweise als negativ klassifiziert wurden (Versäumnis)
- FP (engl. False Positives) - Falsch Positiv: die Anzahl der falschen positiven Klassifizierungen (Fehlaktivierung)
- TN (engl. True Negatives) - Richtig Negativ: die Anzahl der korrekten Ablehnungen
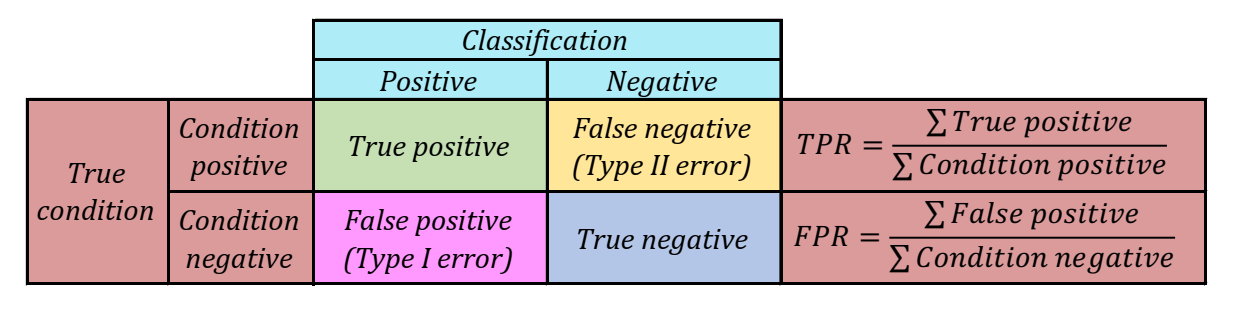
Abbildung 1: Komponenten der Konfusionsmatrix. Man unterscheidet vier Fälle für einen binären Klassifikator. Wenn
der Output des Klassifikation p und der tatsächliche Wert ebenfalls p ist, spricht man von einem True Positive (TP); wenn der tatsächliche Wert dagegen n ist, spricht man von einem False
Positive (FN). Von einem True Negative (TN) spricht man, wenn der Output des Klassifikators und der tatsächliche Wert beide n sind; und ein False Negative (FN) tritt auf, wenn die
Klassifikator Output n ist, der tatsächliche Wert jedoch p ist.
ROC-Graphen
Wenn wir einige Parameter des Klassifikators verändern, beispielsweise einen Schwellenwert, ergeben sich jeweils verschiedene Anzahlen von korrekt positiven und korrekt negativen Klassifikationen. Eine grafische Darstellung der Richitig-positiv-Rate(engl. TPR, True Positive Rate) gegen die Falsch-positiv-Rate (engl. FPR, False Positive Rate), wenn ein Parameter des Klassifikators (z. B. Schwelle) variiert wird, wird als ROC-Kurve bezeichnet (Abbildung 2 zeigt, verschiedene Klassifikatoren in einem ROC-Graphen und in Abbildung 3 zu finden sind.
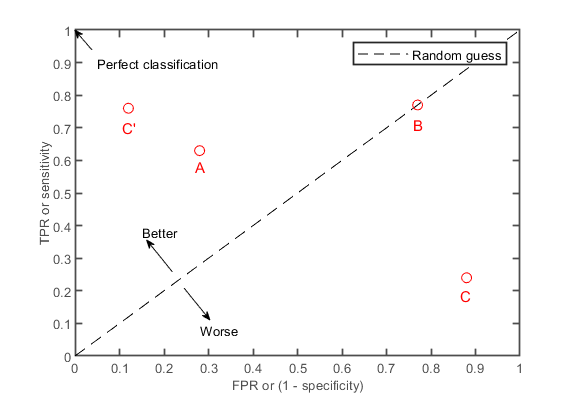
Abbildung 2: Der ROC-Graph. Die True Positive Rate (TPR), deutsch Richtig-positiv-Rate oder Sensitivität, gibt den
Anteil der korrekt als positiv klassifizierten Objekte an der Gesamtheit der tatsächlich positiven Objekte an. Die False Positive Rate (FPR), deutsch Falsch-positiv-Rate, gibt den Anteil
der fälschlicherweise als positiv klassifizierten Objekte an der Gesamtheit der tatsächlich negativen Objekte an. A und C‘ sind Klassifikatoren, die das Zufallsniveau überschreiten. Die
Leistung von Klassifikator B liegt auf dem Zufallsniveau, während Klassifikator C unterhalb des Zufallsniveaus liegt. Ein perfekter Klassifikator erzeugt einen Punkt in der linken oberen
Ecke des Diagramms; dieser entspricht einer TPR von 1 und einer FPR von 0.
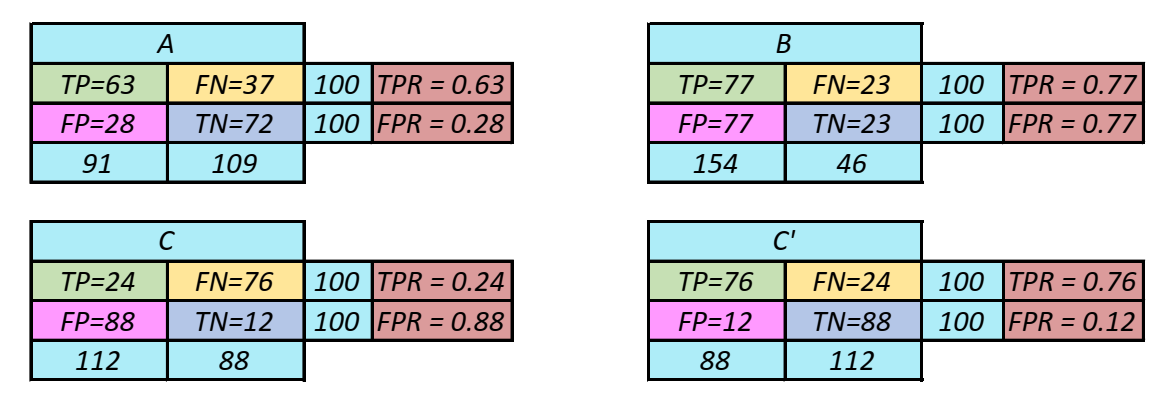
Abbildung 3: Resultate des Klassifikators. Die Ergebnisse der Klassifikatoren sind im obigen ROC-Graphen
dargestellt.
Genauigkeitsklassifizierung
Die Klassifizierungsgenauigkeit \(ACC\) ist als Verhältnis zwischen korrekt klassifizierten Proben und der Gesamtanzahl aller Proben definiert. Daraus folgt: $$ACC = {TP+TN \over TP+FN+FP+TN}$$ Der Wert \(ACC_0 = {1 \over N_Y}\) wird als Chance-Level bezeichnet, wobei \(N_Y\) die Anzahl der Klassen bezeichnet (2 für binäre Klassifikatoren).Kappa-Koeffizient
Der Kappa-Koeffizient ist eine weitere nützliche Messgröße. $$k = {ACC-ACC_0 \over 1-ACC_0}$$ Der Kappa-Koeffizient ist unabhängig von den Stichproben pro Klasse und der Anzahl der Klassen. \(k = 0\) bedeutet eine Klassifizierung auf Chance-Level Niveau; \(k = 1\) bedeutet eine perfekte Klassifizierung. \(k < 0\) bedeutet, dass die Klassifizierung auf einer schlechteren als der zufälligen Ebene erfolgt.Logo - Design - Scripts - Margret Stilke-Volosyak.
1 Wolpaw, Jonathan, and Elizabeth Winter Wolpaw, eds. Brain-computer interfaces: principles and practice. OUP USA, 2012.
2 Rao, Rajesh PN. Brain-computer interfacing: an introduction. Cambridge University Press, 2013.